1- ¿Por qué es importante estudiar las curvas cónicas?
Pues porque son importantes en muchos campos de la ciencia y la tecnología, y su estudio es fundamental para comprender y aplicar conceptos matemáticos y físicos en diversas áreas. Algunas razones por las que es importante estudiar las curvas cónicas son:
- Aplicaciones en la geometría y el diseño: Las curvas cónicas tienen una amplia gama de aplicaciones en la geometría y el diseño, incluyendo la construcción de arcos, puentes, edificios, etc. Además, son importantes en la creación de diseños y gráficos en áreas como la arquitectura, la ingeniería, el diseño gráfico y el arte.
- Aplicaciones en la física y la ingeniería: Las curvas cónicas se utilizan en la física y la ingeniería para modelar sistemas físicos y analizar problemas relacionados con la óptica, la acústica, la mecánica de fluidos y otras áreas. Por ejemplo, la parábola se utiliza en los espejos de los telescopios y las antenas parabólicas, mientras que la elipse es útil para la descripción de órbitas planetarias y la trayectoria de los proyectiles.
- Aplicaciones en la tecnología moderna: Las curvas cónicas son fundamentales para muchas tecnologías modernas, como los sistemas de GPS, las redes de telecomunicaciones y los sistemas de navegación. Por ejemplo, las antenas parabólicas se utilizan en los sistemas de comunicación por satélite, y la elipse se utiliza en la creación de órbitas de satélites artificiales.
Para comprender su estudio es necesario saber qué es un cono, dado que las curvas cónicas surgen al cortar dicha figura con un plano. Dependiendo de la inclinación de dicho plano obtendremos una curva u otra.
2- ¿Qué es un cono?
Un cono es una figura geométrica tridimensional que se puede obtener al girar un triángulo rectángulo alrededor de uno de sus catetos. La base del cono es el círculo que se forma al final del giro, y el vértice es el punto del triángulo que no se encuentra en el círculo de la base.
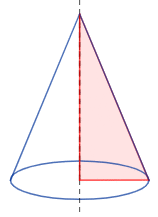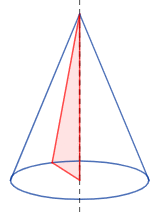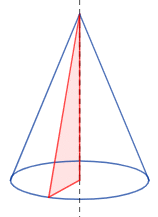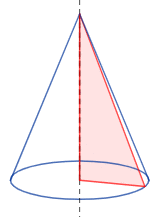
El origen de la forma del cono se remonta a la antigüedad, donde se utilizó por primera vez como forma para crear objetos y estructuras. Los antiguos egipcios, griegos y romanos utilizaron conos en la construcción de edificios y monumentos, así como en la creación de objetos cotidianos como lámparas y jarrones.
En la Edad Media, el uso del cono se expandió en áreas como la arquitectura y la ingeniería, y se utilizó en la construcción de catedrales y castillos, así como en la creación de herramientas y maquinarias.
Hoy en día, el cono se utiliza en una amplia variedad de aplicaciones, como la fabricación de conos de helado, conos de tráfico, embudos, altavoces, y muchas otras formas de productos y estructuras. Además, el cono es una forma importante en la geometría y la trigonometría, y es una figura básica en la creación de otras formas geométricas, como las pirámides y los cilindros.
¿Cuales son los elementos del cono?
- Altura: es la distancia entre el vértice del cono y el centro de la base.
- Radio de la base: es la distancia desde el centro de la base hasta cualquier punto del círculo de la base.
- Generatriz: es la línea recta que une el vértice del cono con cualquier punto de la circunferencia de la base.
- Ápex o vértice: es el punto donde se encuentran todas las generatrices.
- Directriz: la circunferencia de la base.
3- Ahora sí, ya estás preparado para estudiar las cónicas.
Una vez sabes qué es un cono, estudiemos las curvas cónicas. Esta surgen al cortar dicha figura con un plano. Observa este video en el que te lo explico:
En esta imagen puedes ver claramente cómo dependiendo de la inclinación del plano, surge una curva u otra:
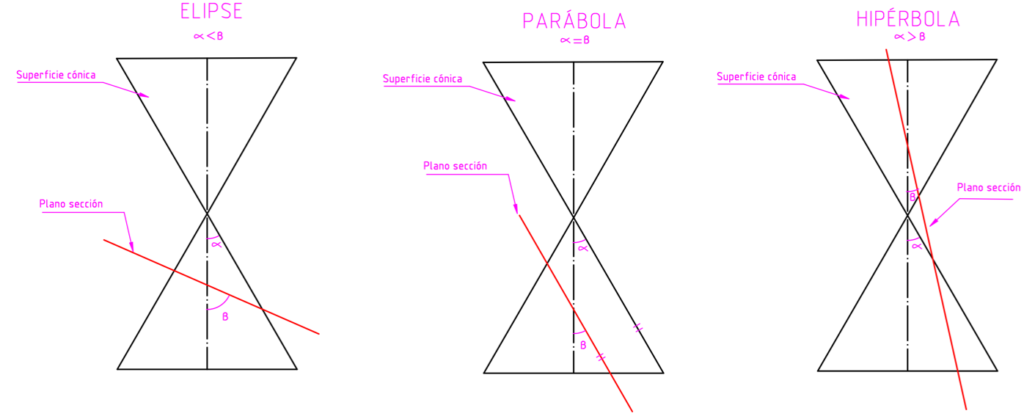
- Si el plano corta a todas las generatrices, pero no es perpendicular al eje, de la superficie la sección será una elipse.
- Si el plano es paralelo a una sola generatriz, la curva tendrá un punto impropio y generará una parábola (curva abierta con una rama).
- Si el plano es paralelo a dos generatrices, tendrá dos puntos impropios por lo que se creará una hipérbola (curva abierta con dos ramas).
Si el ángulo que forman las generatrices con el eje lo consideramos como alfa (a) y al que forma con el plano oblicuo lo denominamos beta (b), la definición de las curvas cónicas quedaría de la siguiente forma:
- Si a < b entonces se genera una elipse.
- Si a = b tendremos una parábola.
- Si a > b se creará una hipérbola.
Todas las cónicas tienen unos elementos básicos comunes:
- Focos: se tratan de dos puntos fijos situados en el eje de simetría que dista 2c entre ellos.
- Eje de simetría: recta sobre la que la curva es simétrica. Sobre ella están situados los vértices (V, V1, V2) de la curva.
- Radio vector: recta que une un punto de la curva con el foco.
- Directriz: intersección del plano de la circunferencia de contacto con el plano de la cónica.
- Circunferencia principal: circunferencia con centro en el centro de la curva y diámetro el eje real.
- Circunferencia focal: circunferencia con centro en cualquiera de sus focos y diámetro el eje real.
- Excentricidad: razón de distancias de un punto de una cónica a un foco y a su directriz. Si esta razón es menor a 1 se obtendrá una elipse, si es igual a 1 tendremos una parábola y si es mayor generará una hipérbola.
Aquí tienes como ejemplo los elementos de la elipse:
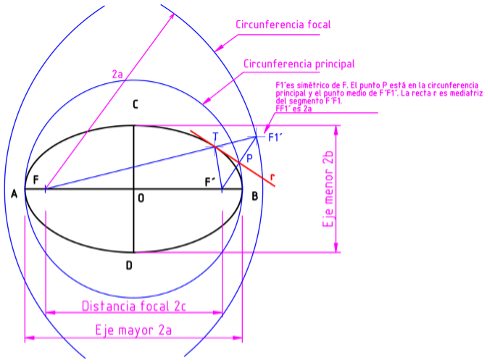
Gran parte de estos estudios sobre las cónicas se las debemos a Apolonio de Perga (262 a.C. – 190 a.C.) el cual fue un matemático griego que estudió las curvas cónicas, incluyendo el cono. Su obra más conocida es «Las secciones cónicas», donde se dedica a estudiar las propiedades y las relaciones entre las curvas que se obtienen al cortar un cono con un plano.
En su obra, Apolonio describe tres tipos de curvas cónicas: la elipse, la parábola y la hipérbola. Estableció las definiciones modernas de estas curvas, incluyendo sus ecuaciones y sus propiedades, y también mostró cómo construirlas geométricamente.
Apolonio también desarrolló el concepto de excentricidad para describir la forma en que un plano de corte atraviesa un cono, y demostró que la elipse y la hipérbola tienen dos focos, mientras que la parábola tiene solo uno.
La obra de Apolonio tuvo un gran impacto en la geometría y en la matemática en general, y sus ideas y métodos siguen siendo estudiados y aplicados en la actualidad. La secciones cónicas de Apolonio se considera una de las obras más importantes de la antigua geometría griega y es una referencia fundamental en la historia de las matemáticas.
4- ¿Qué son los focos de una curva y de donde surgen?
Esta es una pregunta que siempre me he hecho, por eso quería dejarlo por aquí. Seguro que más de uno se lo ha preguntado. Pues aquí tenemos la respuesta y se la debemos a Dandelin:
Dandelin es el apellido del matemático belga Germinal Pierre Dandelin (1794-1847), quien fue uno de los primeros en demostrar el Teorema de Dandelin, una relación entre las secciones cónicas y los conos.
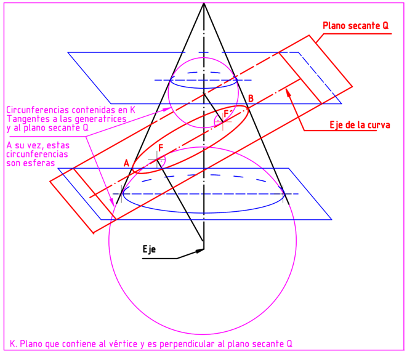
Él demostró que si desde el vértice de la superficie cónica trazamos un plano (K) que contenga al eje y a su vez sea perpendicular al plano secante (Q) que genera la curva cónica, la intersección de ambos planos será el eje de la curva. A su vez, el eje de la curva cortará a la superficie en sus generatrices, dichos puntos de intersección generan los vértices (A, B) de la curva.
Si trazamos circunferencias, contenidas en el plano (K) que contiene al eje, tangentes a las generatrices y al plano secante, los puntos de tangencia de estos dos elementos (plano secante y circunferencias) nos determinan los focos (F, F´) de la curva. Si giramos estas circunferencias sobe su eje, generarán unas esferas tangentes a la curva cónica en los focos de la curva. Por tanto, según Dandelin “podemos definir a los focos de una cónica, como los puntos de tangencia del plano secante a la superficie cónica con esferas inscritas en esta”. Tal vez con este dibujo puedas entenderlo mejor:
Como hemos visto en el primer video de esta entrada, cuando un plano corta a un cono puede generar hasta 4 curvas dependiendo de su inclinación: la circunferencia, la elipse, parábola e hipérbola. La circunferencia ya la conocemos, adentrémonos en el estudio de las otras 3. Haz clic en la curva que deseas estudiar:


